
First, the curve is plotted using “XY scatter”. Microsoft Excel can be used to provide the linear fit (linear regression) for any set of data. Print("LinearFit(Data): ",LinearFit(Data)) RSquared = 1 - sum( - a*Data - b)**2 for i in range(n)])/sum( - 1/n*sum( for j in range(n)]))**2 for i in range(n)]) The “LinearModelFit” can be used to output the of the linear fit as follows: View Mathematica CodeĪ = (n*sum(*Data for i in range(n)]) - sum( for i in range(n)])*sum( for i in range(n)]))/(n*sum(**2 for i in range(n)]) - sum( for i in range(n)])**2)ī = (sum( for i in range(n)]) - a*sum( for i in range(n)]))/n However, these are not covered in this course. The built-in Mathematica function “LinearModelFit” provides the statistical measures associated with a linear regression model, including the confidence intervals in the parameters and. A value closer to 1 indicates that the model is a good fit for the data while a value of 0 indicates that the model does not fit the data. The value of can be calculated as follows: The coefficient of determination, denoted or and pronounced squared, is a number that provides a statistical measure of how the produced model fits the data.
Plt.scatter( for point in Data], for point in Data], c='k')
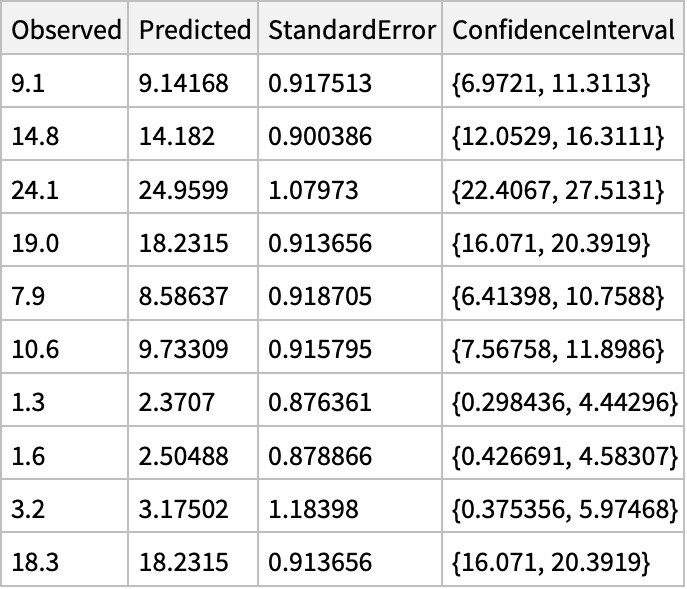
Convergence of Jacobi and Gauss-Seidel Methods.Cholesky Factorization for Positive Definite Symmetric Matrices.


 0 kommentar(er)
0 kommentar(er)
